FCnet

"Fully Convolutional Networks for Semantic Segmentation," Long et al., https://arxiv.org/pdf/1411.4038. This paper is quite important, but I will not be able to fully review it for now. Suffice to say, it involves 'fully-convolutionalizing' multiple different networks and replacing e.g. upsampling operations by transposed convolutions. The whole idea of the paper is to be as fully convolutional as possible, e.g. no linear layers. It's hard to tell if this network uses relu or 1x1 convs, but I think it's the former because:

Note that the deconvolution filter in such a layer need not be fixed (e.g., to bilinear upsampling), but can be learned. A stack of deconvolution layers and activation functions can even learn a nonlinear upsampling... Convnets are built on translation invariance. Their basic components (convolution, pooling, and activation functions) operate on local input regions, and depend only on relative spatial coordinates.

The idea behind this paper in short is to take strong classifiers like alexnet and vgg and then append an upsampling network where normally instead linear layers + a softmax-sampling layer was used, the upsampling network is made up of transposed convolutions so that the whole net is ushaped. Actually, this network also has unet-skips so in many ways it was an enormous contributor of memetic material. Most of the memetic material we associate with unet comes from this paper: the skips, the tconv upsampling. The point of all this is to turn an image classifier into an image-segmentation network. A visual overview of the unet-skip structure is shown (p. 6 in the paper):

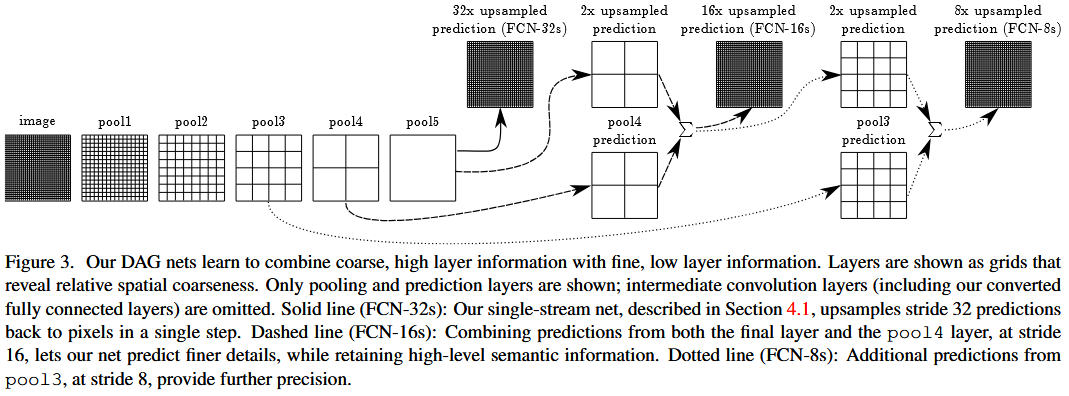
The idea behind the skips is to reintroduce shallower or less processed information at finer levels of locality, with the idea being that the finer levels of locality will need less global information and hence will benefit more from the shallow layer equivalent to it in distance from the bottom of the U shape.